“The Shifts” aka The Three Major Principles of the CaCCSS for Mathematics

According to the California Mathematics Framework there are three Major Principles of the California Common Core State Standards for Mathematics.  They are also commonly referred to as the “shifts”.  Focus, Coherence and Rigor are those three principles.  The shifts are specifically called out, not as more standards, but as a way to support understanding of how the standards are different and allow for a framework for teaching the standards.  

What exactly do each of the three Major Principles mean for instruction?

Focus: Places a strong emphasis on developmentally appropriate concepts and procedures for each grade level. This is the opportunity for teachers and students to “go slow, to go fast”. Discussion, discourse, discovery is allowed to take place while instruction is going on, as well as going deeper into the concept.  Focus allows us to move beyond ‘covering’ the standards.

Documents to Support Focus

The Progression Documents

SBAC Claims, Targets, Standards

Coherence: This connects mathematical concepts across grade levels and links major topics. According to the California Mathematics Framework, “coherence can be used to improve the instructional focus by linking additional or supporting topics to the major work of the grade.” (p.10)

Dr. William McCallum, one of the lead writes of the CCSS explains why Coherence is important in mathematics instruction in this 5 minute video.

Documents to support Coherence

Coherence Map

Rigor: is the term used to reference the idea that conceptual understanding, procedural skill and fluency, and application are all necessary for balanced mathematics instruction.

• Conceptual Understanding involves the teachers and students being able to explain the why and how of the mathematics being learned. Teachers involve students in questioning and justifying their responses, as well as those of their peers.  Each of the grade levels has standards that require students to understand.
• Procedural Skill and Fluency involves students building on their prior knowledge to gain automaticity with their mathematical skills.  The standards are explicit in which fluency is required and at what grade level. Progress towards fluency should be woven throughout the curriculum and the grade levels as students gain confidence in both knowing their facts as well as being able to understand and explain why they work.
• Application of Real World situations.  Allowing students the opportunity to apply their learning to a situation that takes place in the real world is one aspect of rigor and is also one of the Standards for Mathematical Practices, Modeling.

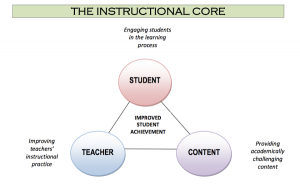
In consideration of the Instructional Core as described by Elmore, what questions, actions or considerations might we need to ask/do about the Instructional Shifts for Mathematics as we continue to improve our mathematics programs for the students in which we serve?